- A.3,2
- B.32/10
- C.10/20
- D.-10/32
- E.-32/10
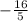 Jawaban:
Jawaban:Pembahasan:
-3,2 karena tempat desimal adalah 1,tambahkan 10 ke penyebut maka menjadi 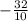 dan bisa disederhanakan lagi menjadi
dan bisa disederhanakan lagi menjadi 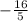 karena dibagi 2.
karena dibagi 2.
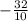 dan bisa disederhanakan lagi menjadi
dan bisa disederhanakan lagi menjadi 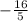 karena dibagi 2.
karena dibagi 2.Kesimpulan:
Jadi,invers perkalian dari -3,2 adalah - 3 2 / 1 0
2. Beras dibeli dengan harga Rp
Jawaban:
HB: 180.000/40KGHJ: 10.000×(40:2)= 200.000Untung: 200.000-180.000=Rp 20.00020.000/180.000×100%=11,1%
Untuk menghitung persentase keuntungan, pertama-tama kita perlu mengetahui nilai beli dan nilai jual dari beras tersebut.
Harga beli beras adalah Rp 180.000,00 untuk 40 kg, yang dapat disederhanakan menjadi Rp 4.500,00 per kg.
Harga jual beras adalah Rp 10.000,00 untuk 2 kg, yang dapat disederhanakan menjadi Rp 5.000,00 per kg.
Selanjutnya, kita dapat menghitung perbedaan antara harga jual dan harga beli, yaitu Rp 5.000,00 - Rp 4.500,00 = Rp 500,00 per kg.
Agar dapat menghitung persentase keuntungan, kita perlu membagi perbedaan harga tersebut dengan harga beli, yaitu Rp 500,00 / Rp 4.500,00 = 0,1111.
Terakhir, kita mengubah nilai desimal menjadi persentase dengan mengalikannya dengan 100, yaitu 0,1111 x 100 = 11,1%.
Jadi, persentase keuntungan dari penjualan beras tersebut adalah 11,1%.
Opsi yang tepat adalah C. 11,1%.
3. Suatu peta dibuat dengan ukuran setiap
4 cm mewakili jarak sebenarnya 48 km
. Jika jarak dua kota 60 km
, maka jarak pada peta adalah …cm.
Jawaban:
Jarak pada peta (JP) = 4 cm
jarak sebenarnya (JS) = 48 km = 4.800.000 cm
Skala = JP : JS
Skala = 4 : 4.800.000
Skala = 1 : 1.200.000
JS = 60 km = 6.000.000 cm
JP = Skala x JS
JP = 1/1.200.000 x 6.000.000
JP = 5 cm
maka jarak pada peta adalah 5 cm
Jelaskan
Dalam soal ini, diberikan informasi bahwa peta dibuat dengan skala 1 cm pada peta mewakili jarak sebenarnya 12 km. Untuk menghitung jarak pada peta, kita perlu menggunakan skala yang diberikan.
Kita diberikan jarak sebenarnya antara dua kota, yaitu 60 km. Untuk menghitung jarak pada peta, kita bisa menggunakan rumus skala. Skala di sini adalah perbandingan antara ukuran pada peta dengan jarak sebenarnya.
Dalam kasus ini, skala peta adalah 4 cm mewakili 48 km. Kita bisa mengubah jarak sebenarnya menjadi satuan yang sama dengan skala peta, yaitu cm. Jadi, 48 km sama dengan 4.800.000 cm.
Selanjutnya, kita menggunakan rumus skala untuk menghitung jarak pada peta. Rumusnya adalah jarak pada peta = skala x jarak sebenarnya. Dalam hal ini, skala adalah 1 : 1.200.000 (1 cm di peta mewakili 1.200.000 cm di dunia nyata) dan jarak sebenarnya adalah 6.000.000 cm.
Substitusikan nilai-nilai tersebut ke dalam rumus, maka kita dapat mencari jarak pada peta. Hasilnya adalah 5 cm.
Jadi, jarak pada peta antara dua kota tersebut adalah 5 cm.
Bentuk sederhana dar
- Bentuk sederhana dari
adalah:
Kita dapat mengurangi pangkat dengan menggunakan aturan pangkat pada kedua suku. Dalam hal ini, kita akan menggunakan aturan pangkat untuk mengurangi pangkat keempat dan pangkat tiga.
Pertama, kita akan mengurangi pangkat keempat dari
Selanjutnya, kita akan mengurangi pangkat tiga dari
Kemudian, kita dapat menggabungkan kedua suku menjadi
Jadi, bentuk sederhana dari
- Bentuk sederhana dari
adalah:
Kita dapat menyederhanakan ekspresi ini dengan mengurangi akar kuadrat dan menyederhanakan pecahan.
Pertama, kita dapat menyederhanakan akar kuadrat
Selanjutnya, kita dapat menyederhanakan pecahan
Kemudian, kita dapat menyederhanakan pecahan menjadi
Jadi, bentuk sederhana dari
- Bentuk sederhana dari
adalah:
Kita dapat menyederhanakan ekspresi ini dengan mengurangi akar kuadrat dan menyederhanakan pecahan.
Pertama, kita dapat menyederhanakan akar kuadrat di dalam pecahan. Kita dapat mengurangi akar kuadrat dari setiap angka di dalam pecahan untuk mendapatkan
Selanjutnya, kita dapat menyederhanakan akar kuadrat di dalam pecahan menjadi
Kemudian, kita dapat menggabungkan suku-suku yang memiliki akar kuadrat yang sama menjadi
Selanjutnya, kita dapat menyederhanakan pecahan menjadi ( \frac{0 \sqrt


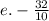
Posting Komentar